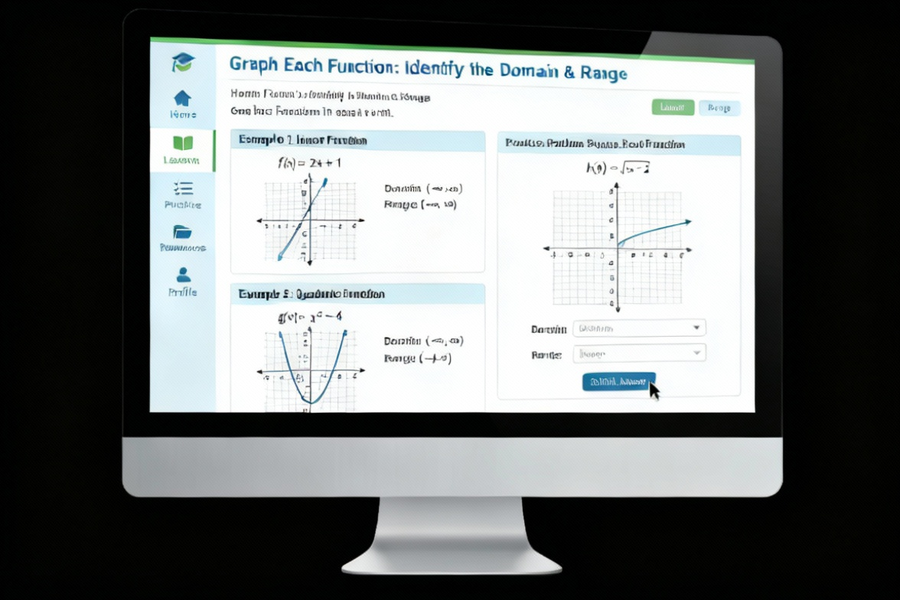
In algebra, every function can be represented visually on a graph. By analyzing the graph, you can determine the domain (all possible input values on the x‑axis) and the range (all possible output values on the y‑axis). Learning how to graph each function and identify the domain and range is essential for understanding how functions behave. Graphs provide a clear picture of the values a function can take, making it easier to apply interval notation and solve problems.
What Is Domain and Range?
- Domain: The set of all possible x‑values for a function.
- Range: The set of all possible y‑values for a function.
For example, the function y=x2 has a domain of (−∞,∞) because any real number can be squared. Its range is [0,∞) because squaring always produces non‑negative results.
How to Graph a Function and Identify Domain and Range
To determine the domain and range of a function using its graph, you first plot the function on the coordinate plane. Once the graph is drawn, examine the x‑axis to identify all the values of x that the graph covers, which represents the domain. Next, look at the y‑axis to see the values of y that the graph reaches, which represents the range. Finally, express both the domain and the range using interval notation, ensuring clarity and precision in describing the sets of values included.
Understanding Interval Notation
- Parentheses ( ) mean the endpoint is not included.
- Square brackets [ ] mean the endpoint is included.
- Infinity (∞) always uses parentheses because it is not a fixed value.
Example:
- x>4 → Domain = (4,∞)
- x≥4 → Domain = [4,∞)
Examples of Graphing Functions
Example 1: Quadratic Function y=x2
- Graph: Parabola opening upwards.
- Domain: (−∞,∞)
- Range: [0,∞)
Example 2: Square Root Function y=x
- Graph: Curve starting at (0,0) and extending right.
- Domain: [0,∞)
- Range: [0,∞)
Example 3: Rational Function y=1x
- Graph: Two branches, one in quadrant I and one in quadrant III.
- Domain: (−∞,0)∪(0,∞)
- Range: (−∞,0)∪(0,∞)
Example 4: Circle Equation x2+y2=r2
- Graph: Circle centered at the origin.
- Domain: [−r,r]
- Range: [−r,r]
Tips for Identifying Domain and Range from Graphs
When analyzing a graph to determine the domain and range, pay close attention to several details. Arrows at the ends of curves show that the graph extends infinitely in that direction, meaning the domain or range continues without bound. Holes or asymptotes indicate values that must be excluded from the domain or range, as the function is not defined at those points. If the graph is broken into separate pieces, combine the different intervals using the union symbol (∪) to represent the complete set of values. Finally, always express the domain and range in order, writing them from the smallest to the largest values for clarity and precision.
FAQs
1. How do you graph each function and identify the domain and range?
You plot the function on the coordinate plane, check the x‑axis for possible input values (domain), and check the y‑axis for possible output values (range). Express both using interval notation.
2. Why is graphing important for finding domain and range?
Graphing provides a visual representation of the function, making it easier to see which values are included or excluded. It helps identify asymptotes, holes, and infinite extensions.
3. Can the domain and range of a function be the same?
Yes. For example, the cube root function has both domain and range equal to all real numbers.
4. How do you write domain and range in interval notation?
Use parentheses ( ) when endpoints are not included and square brackets [ ] when endpoints are included. Infinity always uses parentheses.
5. What are common mistakes when identifying domain and range from graphs?
Forgetting to exclude values at asymptotes, ignoring holes in the graph, or failing to combine multiple intervals with the union symbol (∪).
6. How do you find the domain and range of a circle on a graph?
For a circle defined by x2+y2=r2, the domain is [−r,r] and the range is [−r,r].
7. What tools can help with graphing functions to find domain and range?
You can use graphing calculators, online graphing tools, or algebra software to visualize functions and confirm domain and range values.
Conclusion
To graph each function and identify the domain and range, you must analyze how the function behaves visually. The domain represents all possible x‑values, while the range represents all possible y‑values. Using interval notation ensures clarity and precision. By carefully observing arrows, asymptotes, and breaks in the graph, you can determine the complete set of values. Mastering this process is essential in algebra and calculus, as it helps you understand functions deeply and apply them to real‑world problems with confidence.
Speedy coverage. Thoughtful perspective. Only on QuickFast